Trabajo, potencia y energia. Problemas

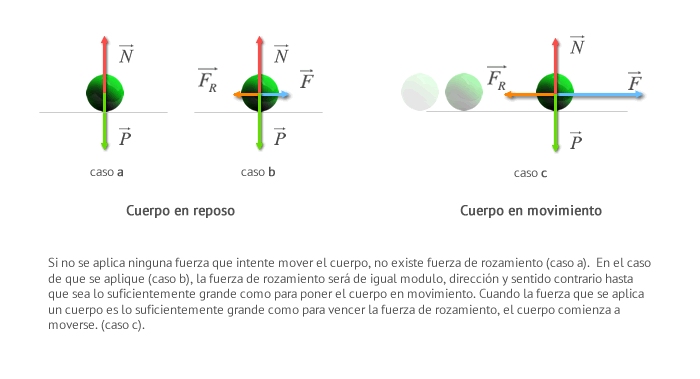
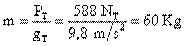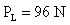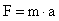En la definición de trabajo cabe destacar dos factores:

1-Sin desplazamiento no hay trabajo

Cuando sostenemos una maleta en la mano, no existe trabajo porque no hay desplazamiento

2-El desplazamiento ha de producirse en la dirección de la fuerza.  Todo desplazamiento perpendicular a la dirección de la fuerza no implica realización de trabajo.

Podemos definir matemáticamente el trabajo como el producto de la Fuerza aplicada por el desplazamiento efectuado, si la fuerza y el desplazamiento tienen la misma dirección:

            Trabajo = Fuerza x Desplazamiento

                                   W =F.∆x

Hay que destacar que  F (Fuerza), es la fuerza neta,  es decir la resultante que actúa sobre el cuerpo, y que en este caso, es una fuerza constante.

Cuando la trayectoria es rectilínea, el desplazamiento coincide con el espacio recorrido y por lo tanto se puede decir que:

Trabajo = Fuerza x espacio

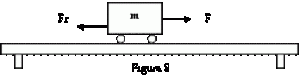
Solamente hace trabajo la componente de la fuerza que coincide con la dirección de desplazamiento. Véase el dibujo:

Si la dirección de la fuerza para mover el baúl forma un cierto ángulo con la dirección del desplazamiento, solo se aprovecha la componente de la fuerza que coincide con la dirección del desplazamiento.

En el sistema internacional SI, la unidad utilizada para medir al trabajo es el Julio (J), que es definido como el trabajo hecho al aplicar una fuerza de 1 Newton, para producir un desplazamiento de 1 metro en la misma dirección de la fuerza.

1 Julio= 1 Newton x 1 metro; 1J=1N*1m

	El Trabajo es máximo y positivo, si la dirección y sentido de la fuerza coinciden con los del desplazamiento El trabajo debido a una fuerza es nulo si las dirección del desplazamiento y de la fuerza son perpendiculares El trabajo es negativo si el desplazamiento y la fuerza tienen sentido contrario (El trabajo hecho por la fuerza de rozamiento es negativo)

3- Concepto de Potencia

Si subimos lentamente unas escaleras y después lo hacemos rápidamente, el trabajo realizado es el mismo en ambos casos, pero  nuestra potencia es mayor en el segundo caso, porque realizamos el trabajo más rápidamente.

Para expresar la rapidez con que hacemos un trabajo, se utiliza el concepto de potencia.

Una máquina es más potente que otra, si es capaz de realizar el mismo trabajo en menos tiempo. La relación entre potencia, trabajo y tiempo invertido se puede expresar de la manera siguiente:

La unidad de la potencia en el Sistema Internacional (SI) es el Vatio (W), que se define como la potencia necesaria para hacer un trabajo de un julio en un segundo:

3.1 Potencia y rendimiento

Supongamos que un motor tiene una potencia Teórica de 1,4 Kw.

Independientemente de ello, el motor invierte 15 segundos en elevar un bloque de 100 Kg. hasta una altura de 16 metros.

Vamos a calcular la potencia real:

Para ello primero calcularemos  el trabajo realizado:

W =F.∆x

W = 100 Kg * 9’8 m/s2 * 16 m =15680 J

La potencia será:

Como podemos comprobar, en la practica la potencia  Teórica y la Real no coinciden (la real es menor), y esto es debido al rozamiento, vibraciones, y calentamiento que sufren los componentes.

Para medir esta perdida de potencia, se define el rendimiento de una máquina como sigue:

En el ejemplo anterior, el rendimiento del motor seria el siguiente:

3.2 Otras Unidades de trabajo y potencia

Unidad de Trabajo:

Se usa muy a menudo como unidad de trabajo el Kilowatio por hora (Kw.h) que se define como el trabajo hecho por una maquina de 1 Kw de potencia durante una hora

Un kilovatio por hora equivale  a tres millones seiscientos mil Julios.

Como unidad de trabajo se suele emplear también el electronvoltio (eV) que equivale a (Es la energía que adquiere un electrón al ser acelerado con una diferencia de potencial de 1 voltio)

Unidad de Potencia

James Watt (1736-1819), ingeniero escocés que invento la maquina de vapor, define también como unidad de potencia el caballo de vapor (CV).

Un Caballo de Vapor podía reemplazar al trabajo que realizaba un caballo en la mina sacando agua (las bombas que extraían  el agua de las minas eran accionadas por caballos).

Un caballo de Vapor equivale a 736 Watios.

4-Energía Mecánica

Como ya hemos visto, un cuerpo tiene energía, cuando tiene capacidad para llevar a término un trabajo.

El trabajo es la manera de expresar la cantidad de energía que ha pasado de una forma a otra forma o de un lugar a otro.

La Energía Mecánica, , suele estar asociada , la mayoría de las veces, con maquinas y movimientos. Esta forma de energía se estudia bajo dos aspectos: energía cinética y energía potencial.

4.1 Energía Cinética

Supongamos que aplicamos una fuerza a un cuerpo de masa m que esta en reposo, el cuerpo se acelera, gana velocidad y recorre una cierta distancia, se hace un trabajo sobre este, el cual se manifiesta en forma de Energía Cinética . Si la fuerza continua actuando sobre el cuerpo, se hace también sobre este un trabajo, que se transforma también en energía cinética.

Calculo de Energía Cinética

Imagina que a un cuerpo en reposo le aplicamos una fuerza F, durante un tiempo, t; el cuerpo se desplaza una distancia, s. Sabemos que:

Fuerza aplicada = masa x aceleración

Como 

Atendiendo que el movimiento es rectilíneo, el desplazamiento coincide con el espacio recorrido:

Como que

Trabajo hecho = Fuerza x desplazamiento

Resulta que:

Decimos que el trabajo llevado a término sobre cuerpo se ha trasformado en energía cinética.

La Energía Cinética se define como la capacidad para efectuar un trabajo por medio del movimiento y de pende de la masa del cuerpo m y de su velocidad, v:

La energía Cinética se expresa en unidad de trabajo (J) Julios

Relación entre Trabajo y Variación de Energía Cinética

Al aplicar un trabajo sobre un cuerpo que esta en movimiento, este aumenta de velocidad. Podemos entonces deducir que:

La variación de la energía cinética es igual al trabajo hecho por la resultante de todas las fuerzas que actúan sobre un cuerpo:

Trabajo = variación de la energía cinética

4.2 Energía Potencial

Todos los sistemas almacenan energía que pueden utilizar en cualquier momento para hacer un trabajo.

Según el dibujo anterior, el chico tiene energía a causa de su posición, al caer, esta energía se transforma en el trabajo necesario para levantar a la chica. Esta energía se denomina energía potencial .

La energía potencial es la que tiene un cuerpo en virtud de la posición que ocupa, que será distinta a la del equilibrio.

Energía Potencial Gravitatoria

El trabajo hecho para elevar un cuerpo hasta una cierta altura se puede calcular de la manera siguiente:

Trabajo = Fuerza (peso del cuero) x Desplazamiento

Por tanto, la energía potencial de un cuerpo de masa m, situado a una altura h sobre un nivel de referencia determinado, se denomina energía potencial gravitatoria.

La energía potencial gravitatoria equivale al trabajo que se hace para elevar un cuerpo hasta una altura determinada (h).

No se puede hablar del valor absoluto de la energía potencial gravitatoria que tiene un cuerpo situado a una altura determinada, sino únicamente de diferencias de energia potencial. De manera convencional, y para evitar este inconveniente, se considera superficie terrestre (h = 0) como el nivel cero de energía potencial.

La energía potencial gravitatoria es proporcional a la masa (m) de un cuerpo cuando este ocupa una posición (h): nada más se modifica al variar la altura.

En un desplazamiento horizontal, la energía potencial no cambia, es decir, en un desplazamiento de este tipo, el trabajo llega a termino porque la fuerza peso es nula.

Energía Potencial Elástica

Como ya sabemos, cuando comprimimos o estriamos un muelle, estamos aplicándole una fuerza F, y se produce un desplazamiento x.

Tenemos una masa, m, unida a un resorte de constante elástica, k , y tomamos como origen de coordenada x, la posición de la masa m, en la que el resorte tiene la longitud normal (sin comprimir o alargar). Estiramos el muelle lentamente en sentido horizontal hasta la posición x.

Los resultados obtenidos se recogen en la grafica siguiente:

Fuerza (N)	Alargamiento (m)
1
2	2.
3	3.
4	4.
5	5.

Observa que la fuerza elástica  F= k.x, no es constante, y por consiguiente, no podemos establecer el trabajo hecho por esta fuerza de la misma manera que determinamos el trabajo ejecutado por la fuerza peso, sino que hemos de calcularlo gráficamente.

El trabajo hecho por la fuerza F no se ha trasformado en energía cinética ni en energía potencial gravitatoria, tampoco hemos tenido en cuenta el rozamiento. El único efecto de esta fuerza responsable del trabajo ha sido aumentar la energía potencial elástica.

La Energía Potencial Elástica es la que tiene un cuerpo elástico (un muelle, una goma…) a causa de su estado de tensión.

La energía potencial elástica es el área comprendida debajo de la línea de la representación grafica de F en función de x:

Para todas las deformaciones que cumplan la ley de Hooke, la energía potencial elástica almacenada  en el cuerpo deformado es proporcional al cuadrado de la deformación.

_PROBLEMAS

Sobre un cuerpo de 10 kg de masa actúa una fuerza de 100N que forma un ángulo de 30º con la horizontal que hace que se desplace 5 m. Si el coeficiente de rozamiento entre el cuerpo y el suelo es 0,2, calcula el trabajo realizado por la normal, el peso, la fuerza de rozamiento y la fuerza aplicada sobre el cuerpo.

La normal y el peso son perpendiculares a la dirección del desplazamiento y, por tanto, no realizan trabajo.

La fuerza de rozamiento se opone al movimiento del cuerpo, por lo que realiza un trabajo negativo.

Para calcular la fuerza de rozamiento necesitamos conocer la normal “N”. De la figura se deduce que N + F_Y=P, de donde: N=P-Fy.

Aplicando la definición de seno y coseno de un ángulo se deduce que:

FY=F.sen30º y Fx=F.cos30º.

El trabajo realizado por la fuerza de rozamiento será igual a:

Sólo realiza trabajo la componente FX de la fuerza aplicada sobre el cuerpo:

2.- Una bomba eléctrica es capaz de elevar 500 kg de agua a una altura de 25 metros en 50 segundos. Calcula:

La potencia útil de la bomba.

Su rendimiento, si su potencia teórica es de 3000 w.

a)

Rozamiento o fricción y problemas

Si empujas una bola sobre una superficie, esta terminará parándose en algún momento. ¿No contradice este fenómeno al Principio de Inercia?. Como no se le aplica ninguna fuerza, ¿No debería seguir moviéndose indefinidamente?

La cuestión a esa pregunta es bien sencilla. El hecho de que la bola se termine parando no contradice este Principio, ya que durante su movimiento existe una fuerza "invisible" que provoca que la velocidad de la pelota vaya disminuyendo: la fuerza de rozamiento. La bola al desplazarse sobre el suelo roza contra él y contra el aire. Este rozamiento produce una pareja de fuerzas que "tiran" en contra del movimiento. 

La fuerza de rozamiento o de fricción  es una fuerza que surge por el contacto de dos cuerpos y se opone al movimiento.

El rozamiento se debe a las imperfecciones y rugosidades, principalmente microscópicas, que existen en las superficies de los cuerpos. Al ponerse en contacto, estas rugosidades se enganchan unas con otras dificultando el movimiento. Para minimizar el efecto del rozamiento o bien se pulen las superficies o bien, se lubrican, ya que el aceite rellena las imperfecciones, evitando que estas se enganchen.

¿No has patinado nunca sobre un suelo recién pulido o encerado? ¿A que no tienes que hacer a penas fuerza para desplazarte bien lejos?

Características de la fuerza de rozamiento o de fricción

A grandes rasgos, las características de la fuerza de rozamiento se pueden resumir en los siguientes puntos:

• Se opone al movimiento de un cuerpo que se desliza en contacto con otro. 
• Depende de 2 factores:
  • la naturaleza de los materiales que se encuentran en rozamiento y el tratamiento que han seguido. Este factor queda expresado por un valor numérico llamado coeficiente de rozamiento o de fricción.
  • la fuerza que ejerce un cuerpo sobre el otro, es decir, la fuerza normal.

¿Cómo se calcula la fuerza de rozamiento o de fricción?

Cuando el cuerpo está en reposo

La fuerza de rozamiento tiene el mismo módulo, dirección y sentido contrario de la fuerza horizontal (si existe) que intenta ponerlo en movimiento sin conseguirlo.

Cuando el cuerpo está en movimiento

Como la fuerza de rozamiento depende de los materiales y de la fuerza que ejerce uno sobre el otro, su módulo se obtiene mediante la siguiente expresión:

donde:

• FR es la fuerza de rozamiento
• μ es el coeficiente de rozamiento o de fricción
• N es la fuerza normal

PROBLEMA

Determina el módulo de la fuerza de rozamiento de un cuerpo de 20 kg de masa que se encuentra sobre una superficie horizontal con un coeficiente de rozamiento de 0.20, si: a) Se encuentra parado. b) Se encuentra en movimiento.

Solución

Cuestión a)

Como hemos visto en el apartado, siempre que un cuerpo se encuentra en reposo, o el módulo de la fuerza de rozamiento es 0 N, o es igual al valor de una una fuerza que intenta moverlo sin éxito.

Cuestión b)

Datos

m = 20 kg
g = 9.8 m/s2
μ= 0.20
FR = ?

Resolución

La fuerza de rozamiento, se calcula por medio de la siguiente expresión:

$$F_R=\mu ·N$$

Conocemos μ, sin embargo necesitamos conocer la fuerza normal N. Dado que se encuentra sobre un plano horizontal:

$$\begin{gathered} N=P=m·g\Rightarrow \\ N=20 kg · 9.8 m/s^2 \Rightarrow \\ \underline{N =\hspace{0.17em}196 N} \end{gathered}$$

Sustituyendo, la fuerza normal en la expresión de la fuerza de rozamiento:

$$\begin{gathered} F_R=0.2 · 196 N \Rightarrow \\ \boxed{F_R=39.2 N } \end{gathered}$$

Segunda condición de equilibrio y problemas

 Equilibrio rotacional

Es aquel que se genera cuando un cuerpo esta pasando por un movimiento de rotación o un giro. Este fenómeno ocurre cuando las torcas ejercidas por las fuerzas que actúan sobre el cuerpo son nulas.

Es aquel equilibrio que ocurre cuando un cuerpo sufre un movimiento de rotación o giro, al igual que el equilibrio traslacional debe también equilibrarse; surge en el momento en que todas las torcas que actúan sobre el cuerpo sean nulas, o sea, la sumatoria de las mismas sea igual a cero.

EMx= 0

EMy= 0

su fuerza se mide en torques o torcas es una magnitud vectorial, obtenida como producto vectorial del vector de posición del punto de aplicación de la fuerza con respecto al punto al cual se toma el momento por la fuerza.Explicado de una forma mas sencilla el torque es el producto entre la fuerza aplicada y la distancia a la cual se la aplica medida, generalmente, desde el punto que permanece fijo.

Así como una fuerza provoca una traslación, un torque produce una rotación.

El torque mide, de alguna manera, el estado de rotación que provoca la fuerza o la tendencia a producir una rotación.Del mismo modo que puede evitarse el desplazamiento de un objeto aplicando una fuerza contraria a la que lo hace mover, puede evitarse una rotación aplicando un torque contrario al que lo hace girar.

Ejemplos de rotacion y su fuerzas aplicadas

CONDICIÓN DE EQUILIBRIO DE ROTACIÓN

Si a un cuerpo que puede girar alrededor de un eje, se la aplican varias fuerzas y no producen variación en su movimiento de rotación, se dice que el cuerpo puede estar en reposo o tener movimiento uniforme de rotación. 

Para que exista este equilibrio se presentan los siguientes factores 

a) Par de fuerzas: Se produce un par de fuerzas cuando dos fuerzas paralelas de la misma magnitud pero en sentido contrario actúan sobre un cuerpo, su resultante es igual a cero y su aplicación esta en el centro de la linea que une los puntos de inicio de las fuerzas componentes.

b) Momento de una fuerza: Llamado también momento de torsión o torque y se define como la capacidad que tiene una fuerza para hacer girar un cuerpo, es decir es la intensidad con que una fuerza tiende a comunicarle un movimiento de rotación. El momento de una fuerza se obtiene multiplicando el valor de la fuerza por su brazo de palanca.

c)Centro de gravedad.

El centro de gravedad (CG) es el punto de aplicación de la resultante de todas las fuerzas de gravedad que actúan sobre las distintas masas materiales de un cuerpo, de tal forma que el momento respecto a cualquier punto de esta resultante aplicada en el centro de gravedad es el mismo que el producido por los pesos de todas las masas materiales que constituyen dicho cuerpo. En otras palabras, el centro de gravedad de un cuerpo es el punto respecto al cual las fuerzas que la gravedad ejerce sobre los diferentes puntos materiales que constituyen el cuerpo producen un momento resultante nulo (dicho punto no necesariamente corresponde a un punto material del cuerpo, ya que puede estar situado fuera de él.

d)Equilibrio estático: existe un equilibrio estático cuando todas las fuerzas que actúan

sobre todos los componentes de un sistema están equilibradas.

e)Vectores: un vector es una magnitud que tiene dos características: módulo, o magnitud,

y dirección. Los vectores normalmente se dibujan como flechas. Una fuerza y el

momento de una fuerza son magnitudes vectoriales

Aplicaciones de el equilibrio rotacional

El equilibrio rotacional se puede aplicar en todo tipo de instrumentos en los cuales se requiera aplicar una o varias fuerzas o torques para llevar a cabo el equilibrio de un cuerpo. Entre los instrumentos más comunes están la palanca,la balanza romana, la polea, el engrane, etc.

Su formula es:

M = F*r

Donde:

M = Momento de fuerza

F = Fuerza que se aplica

r = Brazo de palanca

Problemas de E quilibrio Rotacional

Una persona aplica una fuerza de 90N en el extremo de una llave, como se observa en la figura si la longitud de la llave es de 25cm. Calcula el momento de torsión que se ejerce sobre la tuerca.

M = F*r

M = (90N)(0.25m) = 22.5Nm

Una persona empuja una puerta perpendicularmente con una fuerza de 9N, si el momento de torsión que se produce es de 5.4Nm. ¿Cuál es el brazo de la palanca que utiliza?

M = F*r

Se despeja:

r= m/F

r = 5.4Nm/9N = 0.6m

Primera condición de equilibrio (traslacional) y problemas

                                                  EQUILIBRIO TRASLACIONAL

Seguramente estas familiarizado con la idea básica del concepto fuerza. De tu experiencia cotidiana sabes que aplicas una fuerza cuando jalas o empujas algún objeto. Cuando pateas un balón sabes que aplicas una fuerza. Tal vez creas que la fuerza se asocia con el movimiento, sin embargo, no siempre que se aplica una fuerza se produce movimiento. Si empujas una de las paredes de tu salón de clases verás que no se produce movimiento alguno a pesar del esfuerzo que haces.

.

Decimos que un objeto se encuentra en equilibrio si no esta acelerado. Por tanto el equilibrio considera dos situaciones: cuando el objeto esta reposo o bien cuando se mueve de una velocidad constante en una trayectoria rectilínea

Decimos que un objeto esta en equilibrio traslacional cuando se encuentra en reposo o bien se mueve en línea recta con velocidad constante.

Condiciones de equilibrio: Para que un cuerpo se encuentre en equilibrio, se requiere que la sumatoria de todas las fuerzas o torcas que actúan sobre él sea igual a cero. Se dice que todo cuerpo tiene dos tipos de equilibrio, el de traslación y el de rotación.

Traslación: Es aquel que surge en el momento en que todas las fuerzas que actúan sobre el cuerpo se nulifican, o sea, la sumatoria de las mismas sea igual a cero.

EFx = 0

EFy = 0

Rotación: Es aquel que surge en el momento en que todas las torcas que actúan sobre el cuerpo sean nulas, o sea, la sumatoria de las mismas sea igual a cero.

EMx= 0

EMy= 0

Aplicaciones: Se utiliza en todo tipo de instrumentos en los cuales se requiera aplicar una o varias fuerzas o torques para llevar a cabo el equilibrio de un cuerpo. Entre los instrumentos más comunes están la palanca,la balanza romana, la polea, el engrane, etc.

Problema del equilibrio traslacional

Una caja de 8 N está suspendida por un alambre de 2 m que forma un ángulo de 45° con la vertical. ¿Cuál es el valor de las fuerzas horizontal y en el alambre para que el cuerpo se mantenga estático?.

Primero se visualiza el problema de la siguiente manera:


A continuación se elabora su diagrama de cuerpo libre.

Ahora por medio de la descomposición de los vectores, calculamos la fuerza de cada uno de ellos.

F1x = - F1 cos 45°*

F1y = F1 sen 45°

F2x = F2 cos 0° = F2

F2y = F2sen0°=0

F3x = F3cos90°=0

F3y = - F3 sen 90° = - 8 N*

Porque los cuadrantes en los que se localizan son negativos.

Como únicamente conocemos los valores de F3, F2 y la sumatoria debe ser igual a cero en x e y, tenemos lo siguiente:

EFx=F1x+F2x+F3x=0
EFy=F1y+F2y+F3y=0

Por lo tanto tenemos lo siguiente:

EFx=-F1 cos 45+F2=0

F2=F1(0.7071)

EFy=-F1sen45-8N=0

8N=F1(0.7071)

F1=8N/0.7071=11.31 N

Para calcular F2, se sustituye F1 de la ecuación siguiente:

F2=F1(0.7071)

F2=11.31(0.7071)=8N

Leyes de Newton y problemas

“Las Leyes de Newton”

¿Qué son las Leyes de Newton?

Las Leyes de Newton, también conocidas como Leyes del movimiento de Newton, son tres principios a partir de los cuales se explican la mayor parte de los problemas planteados por la dinámica, en particular aquellos relativos al movimiento de los cuerpos.

Primera Ley o Ley de la Inercia

La primera ley del movimiento rebate la idea aristotélica de que un cuerpo sólo puede mantenerse en movimiento si se le aplica una fuerza. Newton expone que:

Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser que sea obligado a cambiar su estado por fuerzas impresas sobre él.

La primera ley de Newton, conocida también como Ley de inercia, nos dice que si sobre un cuerpo no actúa ningún otro, este permanecerá indefinidamente moviéndose en línea recta con velocidad constante (incluido el estado de reposo, que equivale a velocidad cero).

Como sabemos, el movimiento es relativo, es decir, depende de cuál sea el observador que describa el movimiento.

Así, para un pasajero de un tren, el interventor viene caminando lentamente por el pasillo del tren, mientras que para alguien que ve pasar el tren desde el andén de una estación, el interventor se está moviendo a una gran velocidad. Se necesita, por tanto, un sistema de referencia al cual referir el movimiento.

La primera ley de Newton sirve para definir un tipo especial de sistemas de referencia conocidos como Sistemas de referencia inerciales, que son aquellos sistemas de referencia desde los que se observa que un cuerpo sobre el que no actúa ninguna fuerza neta se mueve con velocidad constante.

De manera concisa, esta ley postula, que un cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo o en movimiento rectilíneo uniforme, a menos que se aplique una fuerza o una serie de fuerzas cuyo resultante no sea nulo sobre él.

Newton toma en cuenta, así, el que los cuerpos en movimiento están sometidos constantemente a fuerzas de roce o fricción, que los frena de forma progresiva, algo novedoso respecto de concepciones anteriores que entendían que el movimiento o la detención de un cuerpo se debía exclusivamente a si se ejercía sobre ellos una fuerza, pero nunca entendiendo como esta a la fricción.

En consecuencia, un cuerpo con movimiento rectilíneo uniforme implica que no existe ninguna fuerza externa neta o, dicho de otra forma, un objeto en movimiento no se detiene de forma natural si no se aplica una fuerza sobre él. En el caso de los cuerpos en reposo, se entiende que su velocidad es cero, por lo que si esta cambia es porque sobre ese cuerpo se ha ejercido una fuerza neta.

En realidad, es imposible encontrar un sistema de referencia inercial, puesto que siempre hay algún tipo de fuerzas actuando sobre los cuerpos, pero siempre es posible encontrar un sistema de referencia en el que el problema que estemos estudiando se pueda tratar como si estuviésemos en un sistema inercial. En muchos casos, suponer a un observador fijo en la Tierra es una buena aproximación de sistema inercial.

Segunda ley de Newton o Ley de fuerza

La segunda ley del movimiento de Newton dice que:

el cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.

La Primera ley de Newton nos dice que para que un cuerpo altere su movimiento es necesario que exista algoque provoque dicho cambio. Ese algo es lo que conocemos como fuerzas. Estas son el resultado de la acción de unos cuerpos sobre otros.

La Segunda ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo. La constante de proporcionalidad es la masa del cuerpo, de manera que podemos expresar la relación de la siguiente manera:

F = m a

Tanto la fuerza como la aceleración son magnitudes vectoriales, es decir, tienen, además de un valor, una dirección y un sentido. De esta manera, la Segunda ley de Newton debe expresarse como:

F = m a

La unidad de fuerza en el Sistema Internacional es el Newton y se representa por N. Un Newton es la fuerza que hay que ejercer sobre un cuerpo de un kilogramo de masa para que adquiera una aceleración de 1 m/s2, o sea,

1 N = 1 Kg · 1 m/s2

2da Ley de Newton: Ley de la Fuerza o Principio Fundamental de la Mecánica

La expresión de la Segunda ley de Newton que hemos dado es válida para cuerpos cuya masa sea constante. Si la masa varia, como por ejemplo un cohete que va quemando combustible, no es válida la relación F = m ·a. Vamos a generalizar la Segunda ley de Newton para que incluya el caso de sistemas en los que pueda variar la masa.

Para ello primero vamos a definir una magnitud física nueva. Esta magnitud física es la cantidad de movimiento que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:

p = m · v

La cantidad de movimiento también se conoce como momento lineal. Es una magnitud vectorial y, en el Sistema Internacional se mide en Kg·m/s . En términos de esta nueva magnitud física, la Segunda ley de Newton se expresa de la siguiente manera:

La Fuerza que actúa sobre un cuerpo es igual a la variación temporal de la cantidad de movimiento de dicho cuerpo, es decir,

F = dp/dt

De esta forma incluimos también el caso de cuerpos cuya masa no sea constante. Para el caso de que la masa sea constante, recordando la definición de cantidad de movimiento y que como se deriva un producto tenemos:

F = d(m·v)/dt = m·dv/dt + dm/dt ·v

Como la masa es constante

dm/dt = 0

y recordando la definición de aceleración, nos queda

Tercera Ley de Newton o Ley de acción y reacción

Con toda acción ocurre siempre una reacción igual y contraria: o sea, las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en sentido opuesto.

La tercera ley es completamente original de Newton (pues las dos primeras ya habían sido propuestas de otras maneras por Galileo, Hooke y Huygens) y hace de las leyes de la mecánica un conjunto lógico y completo. Expone que por cada fuerza que actúa sobre un cuerpo, este realiza una fuerza de igual intensidad y dirección, pero de sentido contrario sobre el cuerpo que la produjo. Dicho de otra forma, las fuerzas, situadas sobre la misma recta, siempre se presentan en pares de igual magnitud y opuestas en sentido.

Tal como comentamos en al principio de la Segunda ley de Newton las fuerzas son el resultado de la acción de unos cuerpos sobre otros.

La tercera ley, también conocida como Principio de acción y reacción nos dice esencialmente que si un cuerpo A ejerce una acción sobre otro cuerpo B, éste realiza sobre A otra acción igual y de sentido contrario.

3ra Ley de Newton: Ley de la Acción y Reacción

Este principio presupone que la interacción entre dos partículas se propaga instantáneamente en el espacio (lo cual requeriría velocidad infinita), y en su formulación original no es válido para fuerzas electromagnéticas puesto que estas no se propagan por el espacio de modo instantáneo sino que lo hacen a velocidad finita “c”.

Es importante observar que este principio de acción y reacción relaciona dos fuerzas que no están aplicadas al mismo cuerpo, produciendo en ellos aceleraciones diferentes, según sean sus masas. Por lo demás, cada una de esas fuerzas obedece por separado a la segunda ley. Junto con las anteriores leyes, ésta permite enunciar los principios de conservación del momento lineal y del momento angular.

Esta ley es algo que podemos comprobar a diario en numerosas ocasiones. Por ejemplo, cuando queremos dar un salto hacia arriba, empujamos el suelo para impulsarnos. La reacción del suelo es la que nos hace saltar hacia arriba.

Cuando estamos en una piscina y empujamos a alguien, nosotros también nos movemos en sentido contrario. Esto se debe a la reacción que la otra persona hace sobre nosotros, aunque no haga el intento de empujarnos a nosotros.F = m a

                                                                         PROBLEMAS

Ejemplo de problemas relacionados con la Segunda Ley de Newton.

• 1. Una fuerza le proporciona a la masa de 2,5 Kg. una aceleración de 1,2 m/s2. Calcular la magnitud de dicha fuerza en Newton y dinas.

Datos

m = 2,5 Kg.

a =1,2 m/s2.

F =? (N y dyn)

Solución

Nótese que los datos aparecen en un mismo sistema de unidades (M.K.S.)

Para calcular la fuerza usamos la ecuación de la segunda ley de Newton:

 Sustituyendo valores tenemos:

 

Como nos piden que lo expresemos en dinas, bastará con multiplicar por 105, luego:

• 2. ¿Qué aceleración adquirirá un cuerpo de 0,5 Kg. cuando sobre él actúa una fuerza de 200000 dinas?

Datos

a =?

m = 2,5 Kg.

F = 200000 dyn

Solución

La masa está dada en M.K.S., en cambio la fuerza está dada en c.g.s.

Para trabajar con M.K.S. debemos transformar la fuerza a la unida M.K.S. de esa magnitud (N)

 

 La ecuación de la segunda ley de Newton viene dada por:

 Despejando a tenemos:

 Sustituyendo sus valores se tiene:

 

• 3. Un cuerpo pesa en la tierra 60 Kp. ¿Cuál será a su peso en la luna, donde la gravedad es 1,6 m/s2?

Datos

PT= 60 Kp = 588 N

PL =?

gL = 1,6 m/s2

Solución

Para calcular el peso en la luna usamos la ecuación

 

Como no conocemos la masa, la calculamos por la ecuación:  que al despejar m tenemos:

 

Esta masa es constante en cualquier parte, por lo que podemos usarla en la ecuación (I):

 

• 4. Un ascensor pesa 400 Kp. ¿Qué fuerza debe ejercer el cable hacia arriba para que suba con una aceleración de 5 m/s2? Suponiendo nulo el roce y la masa del ascensor es de 400 Kg.

Solución

Como puede verse en la figura 7, sobre el ascensor actúan dos fuerzas: la fuerza F de tracción del cable y la fuerza P del peso, dirigida hacia abajo.

 

La fuerza resultante que actúa sobre el ascensor es F – P

Aplicando la ecuación de la segunda ley de Newton tenemos:

Al transformar 400 Kp a N nos queda que:

400 Kp = 400 ( 9,8 N = 3920 N

Sustituyendo los valores de P, m y a se tiene:

F – 3920 N = 400 Kg. ( 0,5 m/s2

F – 3920 N = 200 N

Si despejamos F tenemos:

F = 200 N + 3920 N

F = 4120 N

• 5. Un carrito con su carga tiene una masa de 25 Kg. Cuando sobre él actúa, horizontalmente, una fuerza de 80 N adquiere una aceleración de 0,5 m/s2. ¿Qué magnitud tiene la fuerza de rozamiento Fr que se opone al avance del carrito?

Solución

En la figura 8 se muestran las condiciones del problema

 

La fuerza F, que actúa hacia la derecha, es contrarrestada por la fuerza de roce Fr, que actúa hacia la izquierda. De esta forma se obtiene una resultante F – Fr que es la fuerza que produce el movimiento.

Si aplicamos la segunda ley de Newton se tiene:

Sustituyendo F, m y a por sus valores nos queda

80 N – Fr = 25 Kg. ( 0,5 m/s2

80 N – Fr = 12,5 N

Si despejamos Fr nos queda:

Fr = 80 N – 12,5 N

Fr = 67,5 N

• 6. ¿Cuál es la fuerza necesaria para que un móvil de 1500 Kg., partiendo de reposo adquiera una rapidez de 2 m/s2 en 12 s?

Datos

F =?

m = 1500 Kg.

Vo = 0

Vf = 2 m/s2

t = 12 s

Solución

Como las unidades están todas en el sistema M.K.S. no necesitamos hacer transformaciones.

La fuerza que nos piden la obtenemos de la ecuación de la segunda ley de Newton: 

De esa ecuación conocemos la masa, pero desconocemos la aceleración. Esta podemos obtenerla a través de la ecuación

Porque partió de reposo.

Sustituyendo Vf y t por sus valores tenemos:

 

Si sustituimos el valor de a y de m en la ecuación (I) tenemos que:

• 7. Calcular la masa de un cuerpo, que estando de reposo se le aplica una fuerza de 150 N durante 30 s, permitiéndole recorrer 10 m. ¿Qué rapidez tendrá al cabo de ese tiempo?

Datos

m =?

Vo = 0

F = 150 N

t = 30 s

x = 10 m

Vf =?

Solución

Como nos piden la masa, despejamos la segunda la segunda ley de Newton:

 

 Como no se conoce la aceleración y nos dan la distancia que recorre partiendo de reposo, usamos la ecuación de la distancia en función del tiempo y despejamos (a)

Sustituyendo valores tenemos:

Sustituyendo los valores de X y t en (II) tenemos:

Sustituyendo a y F por sus valores en (I):